原文作者: Ethereum
原文标题: Quadratic Funding: Implementing the revelation principle using SGD
我们认为,在这种情况下,如果有良好的图形界面,直接近似显示(direct approximate revelation)对用户来说更简单,因此进一步增加了生产性协调难度和非生产性协调难度之间的差距。我们描述了一个近似启发过程(approximate elicitation procedure),参考了 Critch 2022[4] 以及一个使用随机梯度下降 (SGD) 的策略执行器(strategy executor),尽管我们可以使用任何全局优化算法,例如 Adam[5]、 Adagrad[6]等。然后我们讨论计算可行性以及如何使策略执行器无需信任和/或保持隐私。
想要进一步了解二次方融资机制背景及相关实践和研究,可查看文末参考文献,DAOrayaki去中心化编辑委员会对二次方机制特作整理。
标准 QF 策略中的信息挑战
Buterin、Weyl 和 Hitzig(2018 年)[7] 指出,“动态实施很可能是可取的 [...],因为最佳贡献仍将取决于其他人的贡献”。换句话说,除非我知道别人贡献了多少,否则我不知道贡献多少,但除非他们知道我贡献了多少,否则其他人不知道贡献多少。但老实说,我不会经常登录来检查和调整我的分配。
让我们说明如果只是简单地呈现匹配(match)的静态预计(可能会歪曲最终匹配)会发生什么。每个项目将从 $0 的静态匹配开始。第一个收到贡献的项目将跳转到 100% 预算的静态匹配。这会随着时间的推移而稀释,但最初的影响是如此之大,以至于它很可能会持续存在,即实际上,被“吸引”来的参与者不会作二次检查然后退出。
直观的结论是,“先行者”(first mover)对公共物品的结果具有不成比例的影响(这可能会因与 UI 排序等相关的先行者优势而加剧)。Gitcoin 的相关数据[8] 初步表明,可能确实存在先行者优势(是否有因果关系需要进一步分析)。
我们能想出一个“智能”预计吗?这样的努力可能会面临全信息限制(full-information constraint),引入中心化的严重偏见,或两者兼而有之。
显示原理
显示原理(Revelation Principle)[9]指出,对于任何机制 m1都有一个“直接机制” m2,直接询问代理人的偏好并为他们执行策略。是否m2比m1更有用,取决于偏好的描述长度(组合拍卖可以作为一个例子[10], 我们通常不想要直接机制)。在 QF 这里,完整的偏好描述是一个连续函数
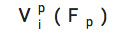 ;但是,我们可以 近似 指定此函数为一维或二维的一些数据点。请注意,我们不考虑联合效用,因为这会增加描述长度;所以,这更适用于相对独立的商品或单一商品的博弈。(见后续文章[11])
;但是,我们可以 近似 指定此函数为一维或二维的一些数据点。请注意,我们不考虑联合效用,因为这会增加描述长度;所以,这更适用于相对独立的商品或单一商品的博弈。(见后续文章[11])
启发(Elicitation)
我们有无数的方法来改善用户界面(UI),但一个简单的界面可能是一个基于点击/拖动的界面,人们可以拖动和/或键入一些
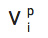
的值。另一个可能是“批量价格”用户界面,用户可以对我们的“批量折扣”出价,直到他们满意为止。我们还向用户解释,他们在项目上花费的金额永远不会超过他们给我们的个人估值。然后我们将使用 任何常见的插值方法[9]并将结果

提交给策略执行器(strategy executor)。请注意,如果给定项目的总边际效用近似值偏离 ,则该项目可能资金不足或资金过剩,因为边际社会效益 (MSB) 将与其他项目相差k。我们预计,随着越来越多的人报告一个给定项目,随机错误近似值(random mis-approximation)将平均化。
这个例子有助于你建立概念,标准 QF 在用户每次登录时都会重新查询用户的出价,因为匹配金额会不断变化。此 UI 会预先查询一个最少的出价集。
该方案类似于 Critch 2022[9] 中介绍的,这也表明一个讨论组件(discussion component)比启发本身更重要。请注意,Critch 2022 通常预设的是高度敬业的个体子集,试图代表整个世界的效用,而不是茫茫多不那么敬业的自私代理人(请注意,任何有效的公共物品募资计划都可能具有前者的一些属性,因为有利于非选民(例如遥远的甚至不远的未来公民)的项目需要无私,并且参与/奉献也遵循 80/20[10] 法则)。Critch 的观点是有道理的,尽管进一步的讨论超出这篇文章的范围。
优化
用户将授权一些支付给机器人,然后机器人将运行梯度下降(gradient descent),模拟用户在频繁检查和调整分配时可能会做的事情。
Buterin、Weyl 和 Hitzig (2018) 还指出,非凹效用(nonconcave utility)是自然的,但会使系统的吸引子非全局(例如“冷启动”效用曲线 - 可视化[11])。因此,我们可以通过使用梯度下降/全局最优化的 随机(stochastic) 变种来实现收益,从这个意义上说,SGD 也可以作为一种 策略修改来诱导相关均衡[12]。
在机制中使用区块链-SGD-协调器可能是一个更广泛的加密经济研究领域。例如,代理人对损失函数的选择(例如, 罗尔斯 vs.功利主义[13])会影响 它选择的均衡[14]( 民间定理[15] 表明均衡选择在许多情况下都很重要),这可能使设计者 能够控制[16] 效率与公平、风险与收益等。一个自然的问题是,人们在同一场游戏(博弈) 的不同协调者之间选边站,元游戏是否会因此产生。
均衡选择问题与维度灾难有关——吸引子的数量和发现它们的难度可能会因人数而急剧增加。我们现在正在优化具有超过数千亿参数的深度学习模型的事实让我们感到欣慰,尽管这种规模的优化成功可能涉及各种前沿技术和手动调整。我们预计优化超过数千到数百万的贡献量不会有很大的问题,特别是如果空间确实是凹的,而且考虑到问题的本质不是黑匣子,我们可以对起点做出有根据的猜测。然而,一旦我们需要证明,计算就会突然变得昂贵起来(鉴于这样的限制,非虚拟化 Cosmos[17] 区块链的共识层计算——如果扩展性足够好,可能带有欺诈证明——可能是不那么雄心勃勃的起点)。我们强调,如果参与者在心理上执行,SGD 算法面临的任何优化挑战将更加严峻(例如,我们认为即使在最简单的场景中,参与者也不太可能发现均衡)。
如果我们使用报告估值的线性插值,离散优化也可能提供优化。我们不需要沿着梯度下降,而是在点之间移动。
交互复杂度
公共物品的性质是,每个物品 i 都与每个参与者 j 相关。因此,系统的交易成本是 X * Y * K,其中 X = 人口,Y = 公共物品选项的数量,K = 交易成本。我们认为,进入效用曲线的 K 低于使用直接贡献博弈的 K,如果 UI 设计没毛病,K 基本上是最小的,瓶颈是 X * Y。由于激励的原因,降采样 X 可能不可行,而对 Y 的随机降采样的改进可能来自同行评审、搜索和个性化推荐。
同意、无需信任和隐私
因为我们授权机器人替我们花钱,所以我们必须强制机器人做正确的事情。这是一个共识和/或证明的用例(尽管可能很贵,参见前面关于计算成本的说明)。
我们也可能希望输入和个人分配是隐私的。SGD 方法实际上更适合差分隐私(这是 同态阈值加密的一个用例[18]),因为计算本质上是最大批量的(maximally batched),即总的最终分配可以直到最后才揭晓。在直接贡献的情况下,我们必须定期更新分配估计(从技术上讲,这做不到,但不这样做,博弈会变成只有一次机会,因此无法玩),这暴露了更新频率和隐私之间的权衡。
鉴于这种隐私能力,我们可能想重新审视 MACI 匿名化[19]。
心理学
有人可能会争辩说,看到一场巨大的和/或夸大的匹配预计,能让人享受参与 QF 的乐趣,比起潜在的机制最优化的扭曲,这是值得的,并且/或者机制的最优化在实践中是一个不切实际的目标(例如,“效用”不是一个清晰的概念)。如果该机制的很大一部分吸引力实际上是其心理效应而不是博弈论效应,那么我们仍然可以报告预计匹配(当然,这将重新引入前面提到的更新频率权衡)。
混合系统
同时具有传统的 QF 体验和 SGD 体验是可能的。在这种情况下,SGD 代理将信息传达给传统参与者会很有帮助,这再一次提醒了我们更新频率的权衡问题。
感谢
感谢 Glen Weyl 的有力反馈,作者后来使用“竞标语言”(bid language)框架对这个概念进行了重大修改和扩展。如果有兴趣,请看 较新的文章[20],不过本文仍可作为一篇很好的背景文章理解。
参考文献
1.DAOrayaki Podcast |二次方治理规模化的现实约束与解法探索
2. DAOrayaki |二次方治理规模化的权衡取舍
3. DAOrayaki |二次方融资与有效利他主义
4. DAOrayaki |二次方融资的社交网络
5. DAOrayaki |基于非货币资本资助的二次方信任模型
6. DAOrayaki |抽签二次方投票
7. DAOrayaki |从默认选择到二次方投票:投票一览
8. DAOrayaki|二次方投票:机制设计如何使民主激进化
9. DAOrayaki|二次方投票和区块链治理
10. DAOrayaki|二次方投票与公共物品
11. 二次方资助V2协议: 抗女巫攻击、公平和规模化的链上二次方投票
12. 累进税系统提高二次方资助的公平性
13. Dora Factory Eric Zhang:使用累进税系统提高二次方资助的公平性
14. 二次方融资(Quadratic Funding)的攻击与防守
15. 社会实验 | 让社区资助爆发巨大能量,当二次方投票遇上黑客马拉松
17. DAOrayaki |Vitalik 最早提出和发表《自由激进主义》3.5w 字全文详解【上】
18. DAOrayaki |Vitalik 最早发表《自由激进主义》3.5w 字全文详解【中】
19. DAOrayaki |Vitalik 等人《自由激进主义》3.5w 字全文详解【下】
尾注
https://anvaka.github.io/fieldplay/?cx=0480000000000005&cy=3.0061&w=13.711400000000001&h=13.711400000000001&dt=0.01&fo=0.998&dp=0.009&cm=1&vf=%2F%2F%20alpha%20%3D%200.5%2C%20V_i%5Ep%28F_p%29%20%3D%20arctan%28F_p%29%0Avec2%20get_velocity%28vec2%20p%29%20%
https://anvaka.github.io/fieldplay/?cx=9.78905&cy=7.32765&w=32.5177&h=32.5177&dt=0.01&fo=0.998&dp=0.009&cm=1&vf=%2F%2F%20Prisoner%27s%20Dilemma%3A%20alpha%20%3D%200.5%2C%20V_i%5Ep%28F_p%29%20%3D%20F_p%20%2F%202%0Avec2%20get_velocity%28vec2%20p%29%20%7B%0A%
https://www.wolframalpha.com/input?i=3d+plot+0.5%280.5%28sqrt%28x%29+%2B+sqrt%28y%29%29%5E2+%2B+0.5x%29+-+x+and+0.5%280.5%28sqrt%28x%29+%2B+sqrt%28y%29%29%5E2+%2B+0.5y%29+-+y%2C+x+from+0+to+1%2C+y+from+0+to+1
https://www.youtube.com/watch?v=yDJ5KiZx7Yw
https://optimization.cbe.cornell.edu/index.php?title=Adam
https://optimization.cbe.cornell.edu/index.php?title=AdaGrad
https://arxiv.org/abs/1809.06421
https://gov.gitcoin.co/t/improving-grant-matching-estimates-during-the-round/7809/3
https://www.youtube.com/watch?v=yDJ5KiZx7Yw
https://en.wikipedia.org/wiki/Pareto_principle
https://anvaka.github.io/fieldplay/?cx=9.78415&cy=6.979699999999999&w=32.5079&h=32.5079&dt=0.01&fo=0.998&dp=0.009&cm=1&vf=%2F%2F%20alpha%20%3D%201.%2C%20V_i%5Ep%28F_p%29%20%3D%205%28arctan%28F_p%20-%2010%29%20-%20arctan%28-10%29%29%0Avec2%20get_velocity%28
https://en.wikipedia.org/wiki/Correlated_equilibrium
https://ocw.mit.edu/courses/14-01-principles-of-microeconomics-fall-2018/88b8835701f40269b3fb5b5e537179a3_MIT14_01F18_lec18_25.pdf
https://en.wikipedia.org/wiki/Equilibrium_selection
https://en.wikipedia.org/wiki/Folk_theorem_(game_theory)
https://www.goodreads.com/quotes/82034-he-who-controls-the-spice-controls-the-universe
https://docs.cosmos.network/main/intro/overview.html
https://protocol.penumbra.zone/main/crypto/flow-encryption/threshold-encryption.html
https://ethresear.ch/t/maci-anonymization-using-rerandomizable-encryption/7054
https://ethresear.ch/t/quadratic-funding-optimal-incremental-revelation-for-the-multi-good-case/13109


