原文作者:Eric Zhang, VegeBun
原文标题:How do hash-based post-quantum digital signatures work? (Part 1)
基于哈希的数字签名方案是后量子数字签名的一个类别。与目前用于验证区块链交易的数字签名方案不同,哈希函数为量子计算机提供的可利用结构要少得多,而且广泛认为它是量子安全的。
目前区块链基础设施上广泛使用的数字签名,如 BLS 和 ECDSA,都是基于离散对数问题。
对于那些不熟悉数字签名的人来说,一个签名方案由四部分组成:系统生成(SysGen),密钥生成(KeyGen),签名生成(Sign),以及签名验证(Verify)。
例如,在 ECDSA 中,公钥 Pk 是通过椭圆曲线群上的生成点 G 来生成的,私钥 Sk 满足 Pk=Sk * G。给定 Pk ,利用经典算法很难找到 Sk。
BLS 签名方案是在配对群
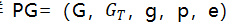
上构建的。公钥/密钥对满足
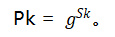
量子算法善于寻找某些函数的周期性,它能发现经典难题的特殊结构,如因式分解和离散对数。当拥有数千个逻辑量子位的量子计算机出现时,BLS、ECDSA 和其他依靠因式分解和离散对数问题的签名方案将不再安全。
例如,求一个数 N=p*q 的素因子可以简化为
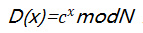
求一个函数的周期。其中 c 是 N 的互素数。一旦找到周期,那么可以通过计算、
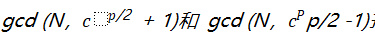
和找到两个互素因子。使用著名的辗转相除法可以很快找到最大公除数,它可以在经典的计算机上运行。反之,在经典计算机上很难找到 D(x) 的周期,但 QPU 可以在多项式时间内完成。
尽管当今的量子计算机只有几百个噪声的物理量子位,但量子计算机的建造者确实拥有大量的路线图来实现大规模的量子计算机。像 IBM 和 Rigetti Computing 这样的超导量子计算机制造商正在向 1000 个物理量子位的量子计算机迈进,并使用可叠加的模块以获得更多数量的逻辑量子位。除此之外,在可预见的未来,还有其他几种方法可以带来有意义的量子计算系统,包括离子阱、中性原子和基于测量的量子计算。
但是,到目前为止,还没有发现有效的量子算法来破解哈希函数,而量子计算机只是将生日攻击速度提高到
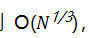
而在经典计算机上的生日攻击速度为
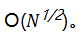
现在让我们来看看如何使用哈希函数来构建数字签名,以及如何处理基于哈希的量子安全签名。
一次性签名方案
首个基于哈希的签名是于 1979 年首次推出的 Lamport 签名。一个 Lamport 签名密钥只能安全地签署一条信息,因此这是一个一次性签名方案(OTS)。该签名方案的工作原理如下:
对于每条信息,签名者需要准备两组密钥对。
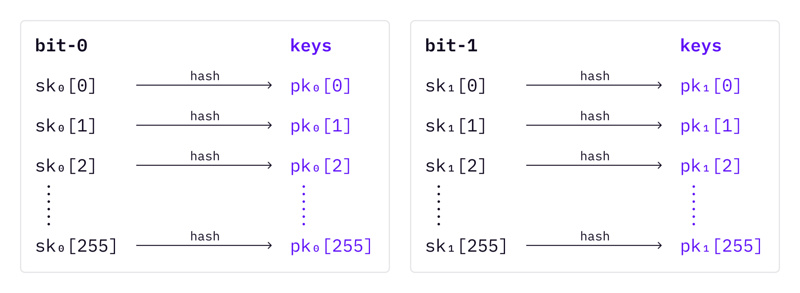
PKs 是通过哈希 SKs 计算的。假设我们使用 256 位的加密哈希函数来产生消息摘要,每组密钥对由 256 个密钥和公钥组成。总的来说,我们需要准备 512 个密钥和 512 个公钥来签署任何一条消息。
要对一个消息签名,首先将消息散列成一个 256 位的随机数;然后,根据散列数的位值,相应地选择 SK。
请注意,我们将始终对消息 h(m) 的摘要进行签名(其中 h 是加密哈希函数),而不是对任意长度的消息进行签名。为了简化标记,我们在本文的剩余部分将使用 m 代替 h(m) 。当你看到 m,即表示着 h(m)。
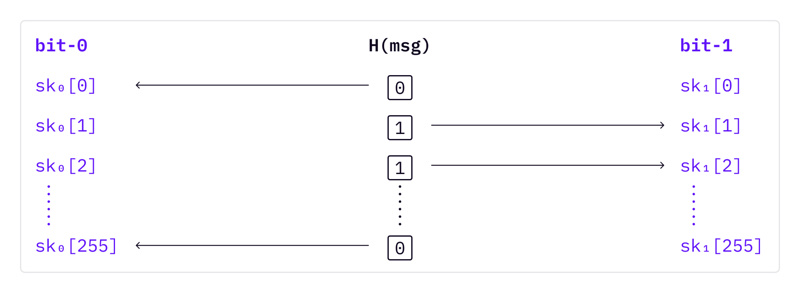
图片注释:签名是
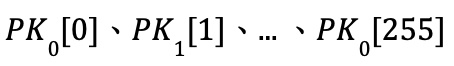
和消息本身。
为了验证签名,首先计算 H(m),然后根据签名计算
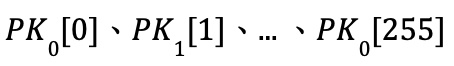
,验证 PK 是否确实是来自 SKs 散列的结果,并且验证索引是否正确。
在对任何消息进行签名之后,该过程都会公开一半的密钥。因此密钥对只能使用一次,否则攻击者将能够使用公开的密钥来验证消息。
使用 Merkle Trees 管理 OTS 密钥
从 21 世纪加密用户的视角来看,Lamport 签名方案乍一看可能很奇怪、很混乱。写下一次私钥或助记词可能就已经给人带来压力和烦恼,如果私钥只能签署一份信息,而每份消息都要共享不同的公钥,这不让人抓狂吗?
事实证明,如果我们能够适当地引入管理密钥的机制和工具,OTS(稍后介绍)签名方案也不是那么糟糕。
因为 Lamport OTS 和 Winternitz OTS 一次只能签署一条消息,如果需要签署多条消息,就必须有多个密钥。Merkle Tree 的签名方案(通常称为“MSS”)是由 Ralph Merkle 发明的,用于管理 Lamport OTS 密钥。
其基本原理是使用 Merkle Tree 的叶子来存储 Lamport OTS 密钥。因为 Merkle Tree 是二叉树,高度为 h 的 Merkle Tree 有
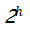
的叶子。如果使用叶子来管理 Lamport OTS 密钥的摘要,那么 Merkle Tree 可以管理
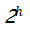
的 Lamport OTS 密钥对。
当签署消息时,需要从树上摘取一个之前从未使用过的 Lamport 密钥对。签名由叶子的索引、Lamport 公钥、Lamport 公钥摘要(叶子)和该叶子的认证路径组成。
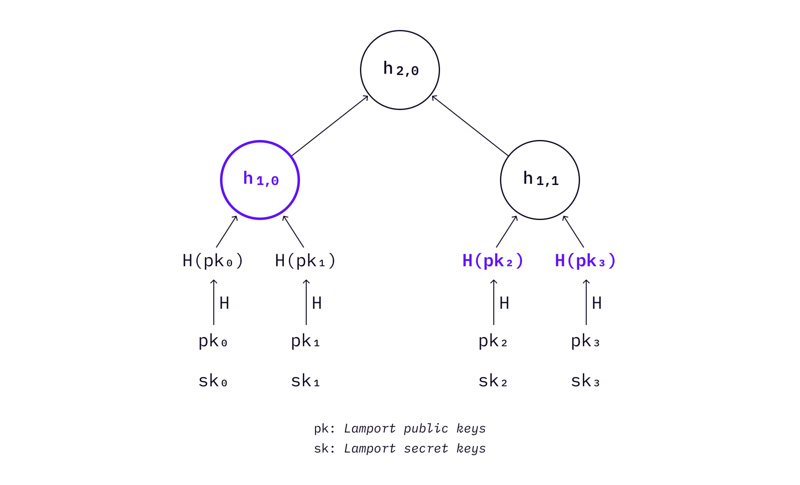
图片注释:在这个简单的 Merkle Tree 中,由
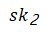
签名的消息是
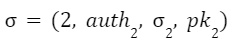
,其中
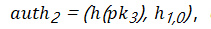
,
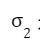
是
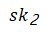
的一半
如果有很多消息需要签名,可以重复上述过程。由 于 Lamport 密钥对是一次性密钥对,因此任何叶子都不能被选择超过一次。因此,MSS 是一个有状态的签名方案。
你可能还注意到,如果验证者只得到一个 Lamport 签名,那么 Lamport 签名方案本身并不能防止中间人攻击。
为了在没有 Merkle Tree 的情况下验证签名者的 Lamport 公钥是否真实,验证者需要保留一份密钥副本。因为所有单独的密钥对都只能一次性使用,因此验证者需要保留一份所有公钥的副本。使用 Merkle Tree 可以有效地让验证者只保存 Merkle 根(Merkle root),而不需要保存
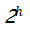
密钥对,从而将空间从
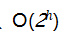
减少到 O( 1)。这意味着,安全地交换一个 Merkle 根就允许多个签名验证。
使用 Merkle Tree 的结果是,每次签名都必须包括认证路径,这是一个更大空间,而且验证者要对 O(h) 计算更多的哈希值来验证每个签名。
Winternitz OTS
Lamport OTS 的另一个问题是,Lamport 公钥和 Lamport 签名太长。Robert Winternitz 提供了一个改进的签名方案(现在将其称为 WOTS),大大减少了签名的大小。
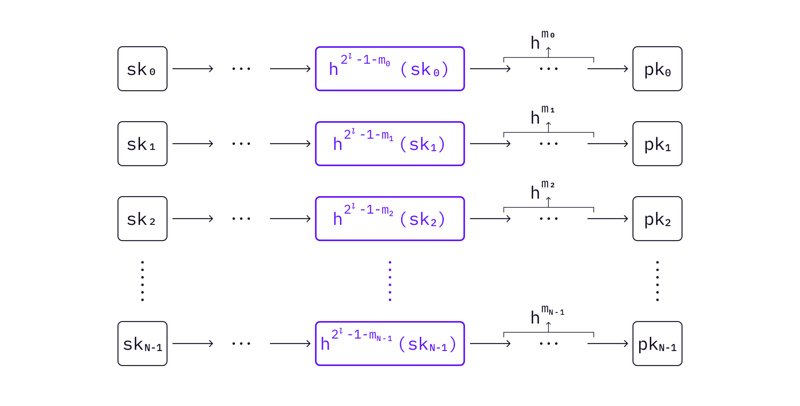
Winternitz OTS 不是为每一条消息准备私钥和公钥对,而是将哈希的消息分成几块。如果一个信息被分成 N 个块,并且每个块有 1 个比特,那么我们就得到了 lenth (m) = N * L。我们将在本文中使用相同的 $l, N& 符号,以便于阅读。
假设我们仍然在信息上使用 256 位哈希函数,并获得信息的 256 位摘要。在这种情况下,N * L = 256 (例如,N = 64 ,l = 4 ,或 N = 8 ,L = 32 ,等等)
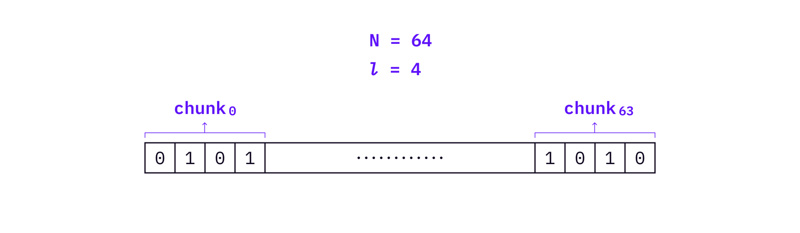
使用上面的例子,m 被分割成 64 个块,每个块有 4 位。所以,WOTS 只需要准备 64 个私有密钥 sk 0 , …, sk 64 。公钥是通过对每个私钥上应用
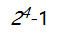
次哈希函数来计算的。
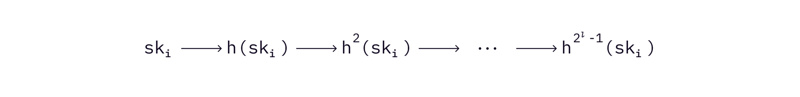
一个 WOTS 签名的生成方法如下。
1、计算消息摘要中每个块的十进制值。例如,第一块的十进制值是 5 。
2、通过将相应的私钥哈希运算计算第
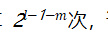
i 个区块的签名。在上面的示例中,sk 0 将被哈希运算次
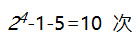
3、对 N 个块应用(1 )和(2 )并生成签名
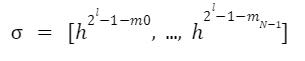
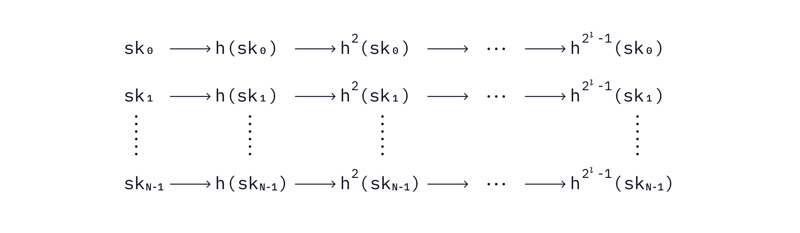
图片注释:每个公钥是通过对相应的私钥哈希运算
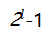
次来获得的。
为了验证签名,验证者将首先对信息进行哈希运算,得到一个 256 位的摘要 m。然后验证者将 m 分成几块,得到每组的十进制值。
然后验证者将签名的每个值哈希运算
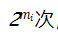
次,得到
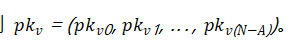
。如果
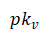
与公钥集 pk 相同,则签名有效,否则签名被拒绝。
WOTS 的折衷方案是在签名生成和验证中增加了更多的计算量。因此,WOTS 的签名将明显比 Lamport 的签名小得多(根据 Merkle 的说法,约为 4 至 8 倍)。
值得注意的是,WOTS 仍然是一个一次性的签名方案,因为一旦使用了密钥对,只要块的十进制值小于原始值,攻击者就可以为每个块生成有效消息。因此,多次使用 WOTS 根本不安全。
WOTS+
WOTS+ 为 WOTS 增加了随机性。它首先向公钥集
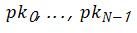
添加了一个额外的公钥
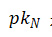
。新的
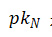
是一组

c 是 WOTS+ 使用的一个哈希函数,它取代了 WOTS 中使用的 h。c 接受两个输入,并递归定义为:
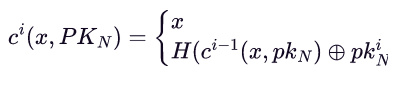
其中 x 是私钥,H 是一个哈希函数。
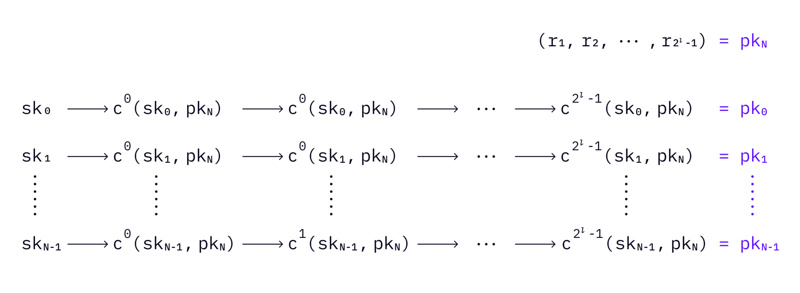
图片注释:WOTS+ 公钥的计算方式与 WOTS 相同,只是将 h 替换为 c,并添加 pkN
WOTS+签名的生成方式与 WOTS 类似,只是做了一些修改。它首先将一个消息 m 分成 N 块
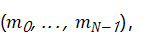
然后计算一个校验和,连接校验和
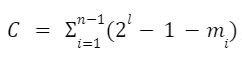
,生成 b = m || c。
计算出签名:
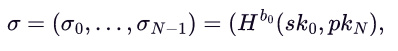
将签名与随机数公式一起发送给验证者。
图片注释:签名是根据
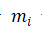
一组中间的方块(哈希值)。
一个签名可以通过对收到的元素进行持续的哈希运算来验证,直到整个 o 集中的每个元素都经过 pk 验证。
具体来说,就是计算
如果
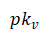
元素匹配 pk,则该签名有效,否则拒绝签名。
尽管 WOTS 和 WOTS 的一些变体使用简单的哈希链,但它们的迭代方法也很常见和简单。然而,WOTS+有一些特殊的迭代模式,可以实现严密的安全性证明,而不需要使用的哈希函数族具有抗冲突性。
扩展的 Merkle Tree 签名方案
因为 WOTS+ 仍然是一个一次性签名方案,如果有多条消息需要签名,那么密钥管理就非常重要。
扩展的 Merkle Tree 签名方案(通常称为 XMSS)使用 Merkle Tree 来管理 WOTS+ 密钥,其方式类似于 MSS 使用 Merkle Tree 来管理 Lamport 密钥。
我们已经知道 MSS 是如何使用 Lamport 密钥对的,所以让我们先看看顶层的 Merkle Tree。
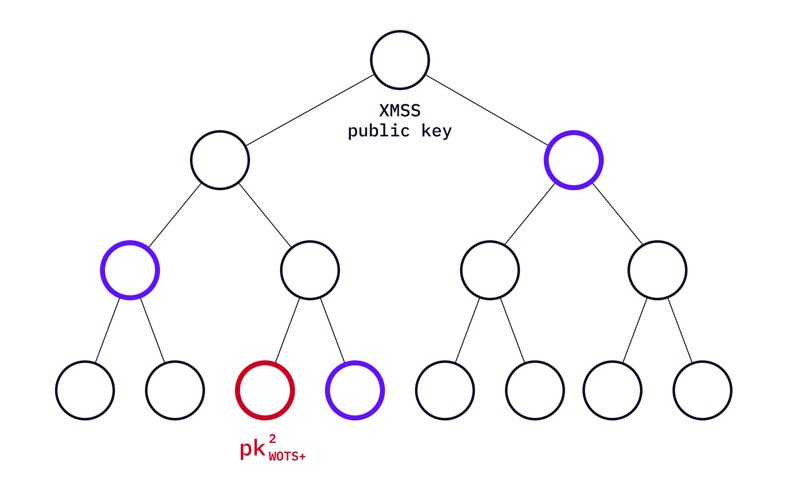
图片注释:用颜色标记验证最终 XMSS 公钥的认证路径
在 XMSS 中,公钥是 XMSS Merkle 根。Merkle Tree 的每个叶子都是 WOTS+ 公钥集的 Merkle 根。为了说明这一点,从上面“扩展”
我们将有一棵“子”Merkle Tree 连接到上面的叶
上。这棵树在文献中也称为“L-tree”。
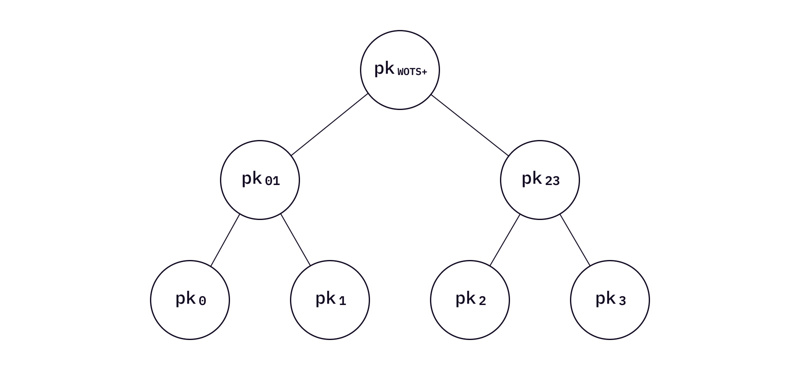
图片注释:一个由 L-tree 管理的 WOTS+ 密钥集。实际树高取决于 WOTS+ 密钥集的大小。
位掩码用于 L-tree。在每次将哈希函数应用于两个节点之前,两个底部值将使用相应的位掩码进行异或运算。L-tree 的每一层都有两个位掩码值
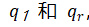
它们将该层的左、右节点进行异或运算。因此,一棵高度为 h 的 L-tree 总共需要 2 h 的位掩码。
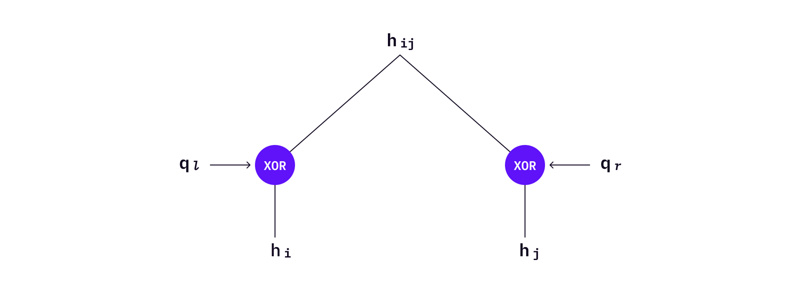
图片注释:L-trees 是如何计算的——在进入哈希函数之前,将一个值与一个位掩码进行异或运算。
现在沿着 L-tree 向下移动—— L-tree 的叶子是 WOTS+ 公钥。每片叶子代表一个 WOTS+ 公钥,该公钥是使用 WOTS+ 中描述的私钥的哈希值链创建。
图片注释:L-trees 是如何计算的——在进入哈希函数之前,将一个值与一个位掩码进行异或。
要对消息 m 签名,首先从 XMSS 树中选择一个由 i 索引的叶子,并确保该叶子以前从未被使用过。然后我们知道该叶子是 WOTS+ 公钥集的一个 Merkle 根。WOTS+ 私钥可以用来对消息进行签名,并得到消息 m 的 WOTS+ 签名
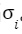
。XMSS 签名

,其中 i 是 WOTS+ 密钥对的索引,
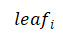
是这个 WOTS+ 公钥集的 Merkle 根。
要验证该签名,首先使用 m 验证
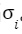
和使用 i 索引的 WOTS + 公钥,然后使用
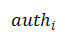
和 XMSS 公钥验证
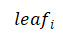
的正确性。
使用 XMSS,可以管理和验证多个 WOTS+ 密钥。
拓展阅读
本文介绍的签名方案是基于哈希的签名方案的基本构建块。Andreas Hülsing 等人在该论文中对基于哈希的签名方案的算法特性进行了更深入的分析。
还有其他以前 NIST 推荐的签名方案(如 Leighton-Micali 签名)和多树方差(如分层签名系统(HSS)和多树 XMSS(XMSS-MT))。NIST 最近的第三轮后量子密码学标准化过程目前不推荐这些签名方案以及本文第一部分所介绍的签名方案。然而,了解这些签名方案的细节非常重要,因为更新的、通常更复杂的签名方案是根据这些算法思想设计的。
本文的第二部分将介绍基于哈希的签名方案的最新发展,包括 SPHINCS/SPHINCS+,以及工程和开源软件的现状。


