一年前,我做了一段时间 Uni V3 的 LP,玩得挺起劲。大约也是那段时间,有一种说法,做 Curve Tricrypto Pool 的 LP 是相当稳健的持续生利的主流资产配置方式,这吸引我阅读了一番 Curve V2 白皮书。对 Uni 和 Curve 两者的气质有了一些朦胧的感觉,是有显著差别的。Uni 追求的是尽可能充分的自由市场,而 Curve 有一些精确的计划经济的气味。
为了推进这个思考,自然有必要把 Curve V2 的技术细节理解透彻,于是几个月前开始仔细研究 Curve V2。作为曾经物理学科研人员的 Curve 创始人,Michael 在白皮书里自如地组合着一个个数学公式。作为数理素人读者,我费力地定位到了其中很核心、却并不直观好懂的元素,Xcp 以及相关的 D、Virtual Price。
研究过程中也意识到,即便高手,亦非一日练成大法,Curve V2 是在 V1 基础上改造后的复杂化、通用化版本。先去理解 Curve V1,能更清晰地把握设计的要义。重走高手当年路。
V1 的主角是 A 和 D。A 参数看似简单,A 越大,在价格1附近分配的流动性越多,一句话就讲完。但当翻阅到当年的记录时(Discord / 治理论坛 / Telegram),不断地蹦出围绕 A 的各种问题,有单纯技术层面的,有和协议治理有关的,林林总总,极为丰富,这也是单写 A 参数的缘起,下文是其中的一部分。首先探讨了 A 作为单个 DEX 的独有参数,对整个市场的影响力。一个有影响力的参数,它的管理便成了个重要问题,下文进一步探讨了调控A的技术细节。
落笔于 A 参数这很微观细碎的话题,倒也没忘了初衷,没忘了对 Uni vs Curve 气质比较的最初兴趣。每每仍在尝试提问,这些细节背后是否透露了一种根本性的理念差别呢?
一. A 参数和全市场价格决定的关系
2020年9月4号,Andre Cronje 在 Curve 治理论坛里发了一个 Proposal,希望把 y Pool 的 A 参数从2000调整到1000。引发了少量的讨论,也有一些反对意见,几天后还是很平静地通过投票了。看着像是没什么重大意义的主题,比起后来很多 DeFi 项目在一些事项上的广泛大辩论,似乎不值一提。
正是 Curve 的数学复杂度抬高了讨论门槛,掩盖了一些问题的重要性,甚至阻碍了对 Curve 本质的理解。本系列文章聚焦于 A 参数,回到上古时期,考察几个历史事件,尝试把数学简化,让关于 Curve 的真正重要的一些命题显现出来。本文是第一篇,以 AC 的这个提案切入。
A 参数可以影响市场价格么?
AC 和反对方的各自陈述
回到 AC 的这个 proposal,8月底9月初 yETH vault 极速扩张( yETH vault 的操作是吸储 ETH,Mint DAI,存入 yDAI vault,也就是存入 Curve y Pool 做 LP,获得 CRV 奖励、卖成 ETH,进而实现 ETH 本位的收益)。
结果正好迎来了 ETH 快速下跌的行情,每当 ETH 急跌,DAI 的需求就大增。y Pool 里面 DAI 的份额跟着极速下降,最低到了只剩2% 的样子。
AC 认为 y Pool 的 A 参数过高了( A = 2000 ),使得 y pool 向市场供应了很多本不该那么便宜的 DAI。比如他的以下论述。

反对声音主要围绕两个角度,其中一个角度和 yETH vault 持续卖出 CRV 带来的抛压有关,这里暂不展开。
令我感兴趣的是和价格决定机制相关的另一个角度。
比如 @iamaloop 的看法:不存在 Cheap DAI,套利者会搬平各处的价格。A 参数只会影响 Curve y Pool 里的币价跟市价齐平后,各个币百分比的失衡程度。
@sjlee 有类似的表达。@angelangel0v 提出,套利者没法因为高的 A 参数就获得更低的价格。
这三位的看法,简要概括就是:DAI 的价格是市场供需决定的,A 参数只能决定 Curve y Pool 在不同 DAI 价格点上的深度、决定不了市场价格。
双方观点的对峙,其实引出了一个问题:A 参数和市场供需的关系是怎样的?
A 参数对供给侧的重要影响
在某些情况下,A 参数在供给一侧有着极其重大的影响,进而是价格决定的最重要变量之一。
在引入供需曲线图之前,先讨论几点重要的前提假设和基本因素。
其一,Curve 是 Passive LP 模式。我的判断是,Passive LP 作为供给方,相对而言更为稳定,即面对变化的行情时,其操作频度相对较低(“操作”指平衡地去存取流动性、或是带有交易属性的单币模式存取流动性,“相对”是相对 Uni V3 的主动管理型 LP 或是 CEX 的做市商)。
其二,Curve LP 的收益很大一部分来自和交易费关系不大的 CRV 代币奖励,在2020年尤甚,且回报率的绝对值较高。那么,面对绝对幅度不大的市场变化时(比如 1~2%),LP 就更加稳定。
以上两点的共同效果是 Curve LP 更加稳定。
其三,对于部分代币,Curve 是最大的流动性阵地。比如2020年的 y Pool 曾是 DAI 的最大兑换池子。
以上三点同时成立的话,会使得全市场的供给曲线主要由 Curve Pool 决定。记住这三点前提,以下便进入供需曲线的讨论。
先看全市场供给曲线,A 值影响了曲线的形状。A 值越高,价格 1 附近的曲线会“越平越长”,流动性越充沛。

全市场供需曲线图
再看需求曲线,我们先假设在平稳的币市行情下的曲线 - 需求曲线1。当 ETH 出现剧跌时,关闭 CDP 的需求急剧上升,市场需要更多的 DAI,因此需求曲线会向右移动 - 需求曲线2。
我们观察供需曲线的交点,可以清晰地看出 A 参数对价格的影响。A 值越低,对应着新的价格均衡点越高。
可见,如果一个代币的主要流动性阵地在 Curve,那么 A 参数对价格决定有着极为重要的影响。
结语
A 参数或多或少地影响了全市场的价格决定,其程度取决于 Curve Pool 代币奖励幅度、Curve Pool 的市占率等因素。
如此重要的参数,很自然地引申出一系列问题。A 参数的设定机制是怎样的?谁来设定,数值的选择标准等。
进一步,市场不是一成不变的,继续引申出一系列动态问题。A 参数什么时候需要调整?调整 A 参数在 AMM 公式层面有何影响?等等
二. 调整 A 带来的曲线变化及损益
2020年4月17日,离312已一个多月,DAI 依然是正向脱锚状态,价格在1.02 左右。
Michael(Curve 创始人)在推特上发起了一个投票,看大家是否支持把 Compound pool 的 A 参数从900调到400。

49人参与了投票,但回复者仅一人。8个小时后,Michael 把 A 调到了400,又发了一则推特,0回复。
在那个当下,能真正参与讨论这个议题的,寥寥无几。Michael 可能沉浸在一个人的试验之中,调试参数、观测、改进,在 Telegram 的只言片语中,我感受到了他的兴致和乐趣。
回到这次 A 参数的调整,带来了日化约0.1%的损失。

我的这一篇,就是想讲清楚 A 调整了之后,到底意味着什么?为什么会带来损失?
不同 A 值对应曲线的一个图示
我挑选了一组实际参数设定,进行图示呈现。本文的讨论对象是 Curve V1 Pool,曲线公式见 V1 白皮书。
黑色曲线对应的参数为:A = 10 D = 20,000
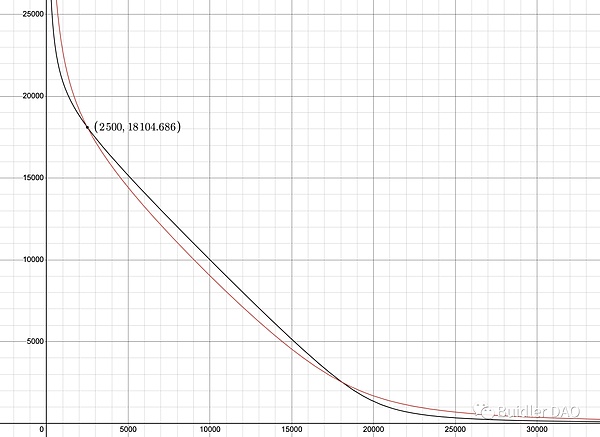
当前池子处于黑色点,X_token、Y_token 的数量分别为 2500 / 18105,价格约为1X_token = 1.36 Y_token。
此刻将 A 降为3,曲线将变成红色线。这条曲线的参数为:A = 3 D = 19,022
比较红黑二曲线,很明显的,黑色曲线中趋近直线的比例更多,这也是 A 之核心作用,A 越大,价格1附近的流动性越多;黑色曲线的 A(10)高于红色曲线的 A(3)。相应地,远离价格1的区间的流动性,则是红色曲线要多过黑色曲线。
在那则推特投票的时刻,DAI 有些脱锚,如果是使用低 A 值的红色曲线,就能比高 A 值的黑色曲线提供更多的流动性,这也是 Michael 想调整 A 的原因,他希望池子能捕获更多手续费。
我们再回到将 A 降为3带来的变化,降为3的那个瞬间,池子内两种 Token 的数量并没有变化,但 D 值发生了变化。此外,图中还能看出,当前点的切线斜率发生了变化,曲线形状亦发生了变化。
以下专门探讨这些变化。切线斜率、曲线形状的变化,若换一角度考察,会更加直观。D 值的变化,则涉及到了池子损益评估的话题。
订单簿视角来看 A 值调整后的变化
Curve 池子可以从订单簿的角度去理解。单个池子,根据其 A、D 参数的不同,对应着在所有价格点上的挂单数量的不同分布,并且所有的挂单是联动的、整体性的存在。
上一节的案例里,当 A 从10降为3的瞬间,可以理解为所有的挂单瞬间做了一次整体性大调整,从黑色的一组挂单集合转换成了红色的挂单集合。
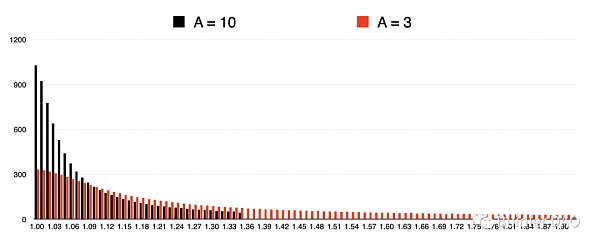
先对上图做一些基本说明。
横轴是价格,1.00 代表 1 X_token = [ 1.00 ~ 1.01 ) Y_token,1.01 代表 1 X_token = [ 1.01 ~ 1.02 ) Y_token,以此类推。为了节省空间,我将价格 < 1.00 的挂单略去了。
竖轴表示 Y_token的数量(即对 X_token 的买单挂单)。黑色部分在价格 > 1.36的区间没有数据,这是因为在黑色曲线上的当前价格是 1.36,> 1.36 意味着 X_token 的更高价卖单挂单。这张图仅考察使用 Y_token 进行买入挂单的部分,因此 > 1.36 的部分无数据。
我们看黑红的对比。首先,当前价格发生了变化,对应着前一节提到的切线斜率的变化。A 调整后,当前价格瞬间变动到了1.92,红色部分的挂单延展到了 1.92。也就是说,有一定数量的 Y_token 在1.36 - 1.92的价格区间内分批挂出了对 X_token 的买单。
这其实是很奇怪的变化,一个 DEX 的当前价格在没有 Swap 的情况下,竟然发生了变化。我们立刻可以想到,这将形成和市场价格的价差,我们假设套利者会瞬间介入把价格打到1.36。
此外,可以看到从1.00 - 1.36的每一个价格点上的挂单数量都有所不同,整体而言,高位挂单的数量更多。这对应着上一节提到的曲线形状的变化。
A 调整带来的损益 - 最直接的计算方式
Michael 的推提及了 Compound Pool A 参数的调低会带来一些损失( ‘Wipe One Day’s Profits’ )。在讨论背后的数学关系之前,需要先把“损失/损益”定义清楚。

按照最直接的想法,定义损益很简单,将两个 Token 的价值折算成 U 或是其中任意一个(X_token 亦或 Y_token),二维转一维,然后对比 A 调整前后的总价值。这也是 Michael 提到的 ‘With Impermanent Loss’。
不妨先简要讨论这个意义上的损益。为求简化,所有的讨论暂且假设手续费 = 0。
还是基于前文一直用的示例,A 调低后,X_token 的瞬时价格变高,套利者介入,把价格打回 A 调整前的价格,这便会带来损失。道理很简单,上一节提到,A 调低后,相当于按照高于市场价的价格挂了很多对 X_token 的买单,这些不正常的买单被套利者吃掉,这必然会带来损失。
从曲线图上看得会更加清晰。

黑色点和黑色曲线是调整前池子的状态,对应价格为1.36 。A 调低后,池子按红色曲线运行,调低的瞬间,池子价格变成1.92,套利者介入使得池子的状态很快从黑色点移到红色点,对应着1.36的价格。
需要比较 A 调整前后的池子总价值,方法比较简单。
先看 A 调整后的总价值(套利者介入后)。找出红色曲线在红色点处的切线和 Y 轴的交点,即为两种 Token 按现价折算成单一 Y_token 的数量。
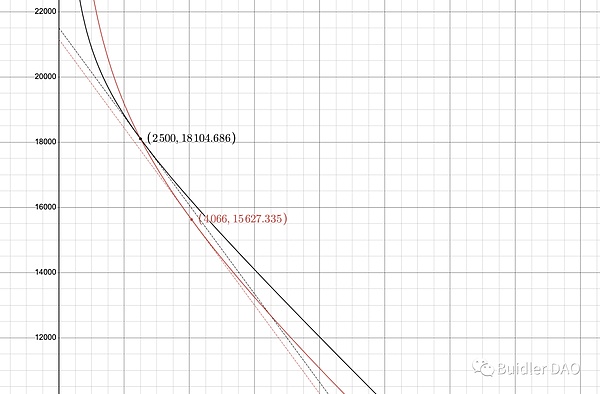
再看 A 调整前的总价值。找出黑色曲线在黑色点处的切线和 Y 轴的交点。因为 A 调整前后的价格是一样的(套利者介入后),因此这条切线和第一步里的切线平行。
显然,黑色切线与 Y 轴的交点更高,也就是 A 调整前的总价值更高。A 调低带来了总价值的损失。
以上讨论仅限于 A 调低后的瞬时损失,还算简单。但若把追踪时间拉长,想探讨后续不同价格走势下 A 调低所带来的长期损益,就变得有些复杂。这取决于价格往更加脱锚的方向去发展、还是回归完美的锚定,A 调整后的总价值可能会不如不调整 A 的状态、也有可能会高过。这里暂不展开,本文的目的仅在简要演示一番 A 调整是如何影响到池子总价值的,并不求完整系统的论述。
剔除无常的损益评估
按照两个 Token 的当前价格折算,也就是考虑进无常,这是最直观的度量方法,但这种方法较为麻烦。Curve 引入了另一种独特的损益评估法,剔除了无常的因素,简化了计算,在大部分情况下也能够适用。
这就是 D 值,D 值是 Curve 曲线公式在 A 之外的另一核心参数。我们在 Curve 官网每个池子里看到的 Virtual Price 即为根据 D 值计算得出。
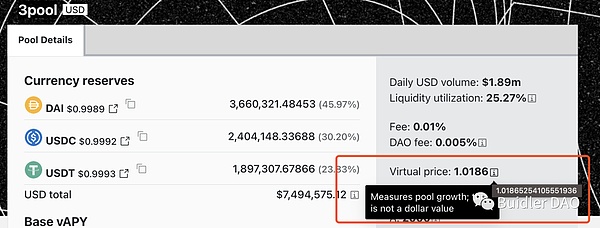
D 值,就是当池子价格是 1(完美锚定)的时候,池子内两种 Token 的总数量。因为此刻价格是 1,因此可以把两种 Token 的数量简单相加。池子价格等于1的点,即为曲线和 x=y 这条直线的交点。
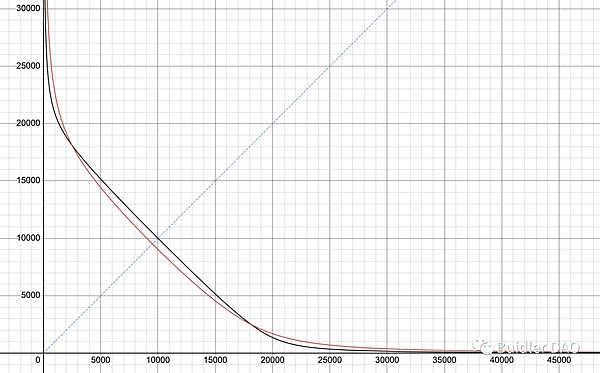
回到前述示例,A 调低以后,很显然,D 值变小了。因此,长期来讲如果价格能够恢复锚定的话,D 值的变化能够反映出因为 A 调整带来的损失。
我上文使用的示例中,当前价格是1.36,这其实是比较极端的情况。我们看 Curve V1 类池子,比如主流的稳定币/ LSD 池子,价格都不会偏离1太多。在价格接近1的时候,无常的影响很小,因此可以直接用 D 值的变化来近似反映损益。
D 值,作为一维的度量衡,且作为池子的参数之一,便于计算、便于追踪历史数值,比较适合用来近似地评估损益。
结语
A 参数的调整相当于在订单簿所有价格点上的挂单的一次重排,改变了当前价格点,改变了 D 值,带来了损益。
因此,A 参数的一次性大幅调整有一种突兀感,甚至有一种瑕疵感。白皮书内对 A 的动态管理并无涉及,或许是在 Curve 上线实际运行了一段时间后,Michael 才渐渐认识到了对 A 参数的调整方式需要修正。在宣布 Compound Pool A 参数调整完毕的那则推特下,Michael 跟了一句评论。后续新版本的池子,A 参数的调整改成了一段时间渐变完成的模式。

老池子 A 参数的一次性调整方式仅仅是瑕疵感么?没这么简单,背后还深藏了一个可被攻击的点。幸运的是,发现这个脆弱点的是白帽(对协议理解的深度真是天外有天)。后续会单写一篇讲述这个攻击方法。


