作者:Steven Yue,原刊于作者知乎
上一期的文章中,我们一起了解了格密码学到底是什么,随后我们学习了LWE问题的构造。最后,我们把所学的内容组合起来,构成了格密码学中最经典的Regev加密算法。(详情点击《初探全同态加密:FHE的定义与历史回顾》)
希望看到这里,大家已经对上期讲到的内容已经有一个深刻的认知了。这一期,我们就可以真正开始实战最后的boss——开始构造全同态加密系统。
上期回顾
在开始之前,为了便于大家能够更好理解这期会描述的FHE系统,我们在此快速的复习一下之前两期文章讲到的比较关键的知识点。
LWE问题
上期文章中较为重点的内容就是LWE问题了。可以说正确的理解了LWE,格密码学和FHE问题就已经搞定了一大半了。

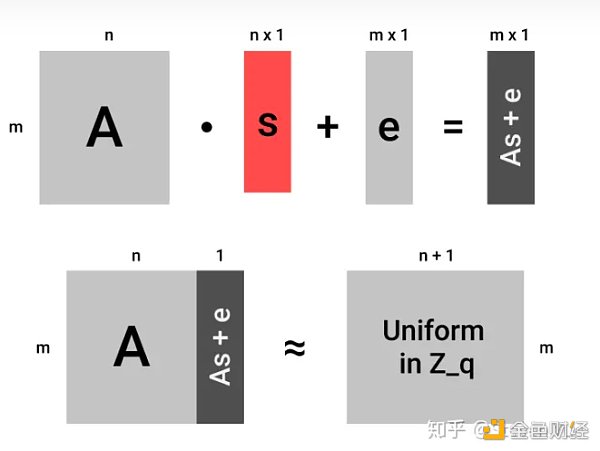


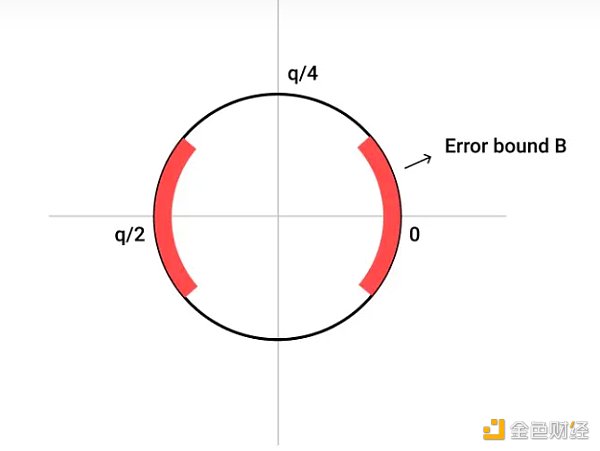

全同态加密体系
最后,我们一起来回顾一下上上期讲到的,一个完整的全同态加密(FHE)体系的构造。
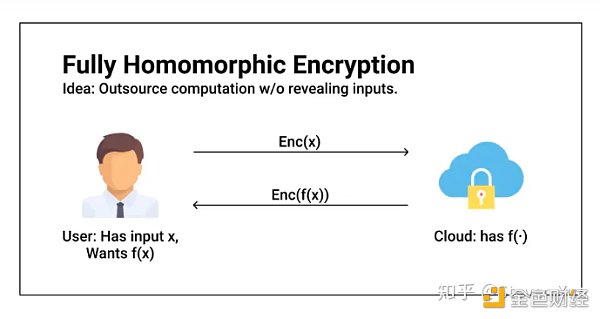


FHE的四个阶段
我们在第一期的文章中,还学习了构成FHE系统的四个不同阶段:
部分同态(Partially Homomorphic Encryption):在这一阶段下,我们可以运算的功能F只能够要么由加法/线性组合,要么由乘法构成。常见的例子有RSA(乘法同态)以及ElGamal(加法同态)。
近似同态(Somewhat Homomorphic Encryption):这一阶段的算法拥有不完整的同态属性,比如拥有Pairing配对的ElGamal循环群,具有完整的加法同态属性,但是只有非常薄弱的乘法同态属性。
有限级数全同态(Leveled Fully Homomorphic Encryption):这一阶段的算法可以同态运算任意形式的功能F,但所转换成的电路的复杂度不能超过上限L,不然就会噪音太大丢失信息。
全同态(Fully Homomorphic Encryption):最后的阶段就是我们想要得到的FHE了。在这一阶段我们可以计算任意复杂度的功能F,
并且噪音可以被完美的控制在可控范围内。
我们之前还提到了,通过Bootstrapping的方式,可以有效的将一个有限级数全同态(LFHE)的系统转换为一个全同态(FHE)的系统。Bootstrapping这一概念是FHE界的开山鼻祖Craig Gentry在09年的PhD毕业论文中指出的。我们这次要讲到的GSW系统,就是一个FLHE系统,随后通过Bootstrapping被有效的转换为FHE系统。
综上所述,我们这一期来仔细的探讨一下,GSW中提出的LFHE系统是怎么构造的吧~
PS:这一段回顾的内容仅仅是前两期描述的一小部分。所以如果大家看到这里对FHE的定义与LWE问题还是不够了解的话,不妨再回去看看之前的文章,然后再回来继续往下看。
构造GSW-LFHE系统的三次尝试
GSW系统是Gentry,Sahai,Waters三位大牛在2013年提出的第三代同态加密系统。整套加密系统围绕了一个核心概念:矩阵的近似特征向量。
乍一听,这个概念有点云里雾里的。所以整篇论文其实也分了三个阶段,循序渐进的来介绍这一系统的构造。这三个阶段中,每一个阶段都提出了一个LFHE系统的尝试,并且评估了这一尝试是否可行。
话不多说,我们这一期就来详细的学习一下Gentry在原文中对于LFHE构造的三次尝试,并且逐步的推导出最后GSW系统的全貌吧。
第一次尝试:矩阵的特征值与特征向量




“加密算法”的问题
我们的第一次尝试就完美的实现了全同态的所有要求,似乎看上去可以直接收摊,结束这篇文章了。
但是我们不能高兴的太早,因为这一体系有一个非常致命的弱点。如果细心的读者朋友们会发现,我们在讲述第一种方案的时候,一直给“加密”二字打上了引号。

但是这一架构对于我们后续的尝试是一个很好的启发,我们缺哪里补哪里就行了。上一期的文章中,我们讲到高斯消除法可以很好的找到线性方程组的解,但是如果我们叠加了一个噪音的话,就变成了困难的LWE问题。我们这里不妨也做同样的尝试,在特征向量与特征值的等式中加入噪音,看看会不会有所变化。










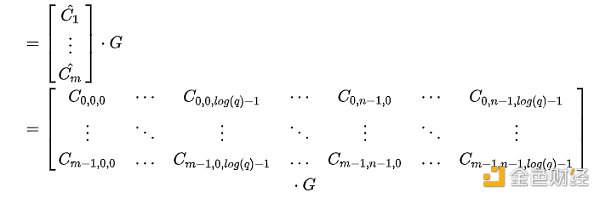









篇尾小结
相比起前两篇文章来说,这一篇文章可以说是最学术、数学公式最多的了。我尽可能地在描述的过程中用大白话来讲述LFHE系统的构造。如果大家在看的过程中还有一些疑惑,不妨把有困惑的地方再读一遍,或者私信我一起交流!
我在文章开头有所提到:GSW系统的精华就在于近似特征向量这么一个定义。我们从普通的特征向量出发构建了一个全同态、但是不加密的系统;随后,我们加入了LWE问题中类似的噪音向量,构成了一个部分同态、但加密的系统。最后,我们使用二进制分解这么一个工具,构成了GSW中最后提到的有限级数全同态加密系统。
看到这儿,如果你已经能get到GSW系统在做什么,是怎么来的的话,恭喜你已经掌握FHE系统构造的精髓啦!这是一件值得高兴的事情,因为FHE是一个相对来说非常年轻(~10年)的领域,我们已经站在密码学技术很前沿了。
下一步,是什么?
我们现在已经根据GSW这一篇paper所述的,一起构建出了一套LFHE系统了。但是就像我在第一篇中承诺的——我们要再接再厉,冲向真正的FHE。
(注:GSW的paper中讲到的加密算法和我们本文中提到的可能有所出入,使用的是一种非对称的形式,而我们用的是对称加密形式。但是这并不会影响整个体系的正确性或者是功能性。个人觉得这样更好理解一点。)
为了能够把LFHE系统转换为真正的FHE系统,我们就需要用到Gentry大佬提出来的Bootstrapping这一方法了。简单的来说,Bootstrapping可以把一个即将达到临界值的、带有很大噪音的密文,”刷新“成一个噪音很小的密文,这样就可以无限制的进行同态运算了。
下一期,我们详细的介绍一下GSW系统中是如何应用Bootstrapping把原本的LFHE转换为FHE的。篇幅允许的话,我们还可以来探讨一下现有FHE库(如HELib,SEAL,TFHE)等的区别。下期见啦~


